Jeremy S. DeBonet & Chris Stauffer: Using Charged Particle Systems To Simulate Fluid Flow
PROJECT PROPOSAL
PROJECT PROPOSAL
We plan to do a particle based simulation of water interaction, including water-water and water-solid interactions. By accurately modeling the attractive and repulsive forces between particles(H2O molecules and other solid particles), our simulation will exhibit such behavior as cohesion, adhesion, and wave propagation.
Most attempts at water simulation have been based on simulation of only the water surface. This however cannot fully capture the dynamic nature of water. To compensate for this, simulations have used the "hack" of adding particles when the model requires a break in the water surface. This duality is apparent in in the resulting images.
MODELING
MODELING
Computing all the interactions between the huge numbers of molecules required to model water accurately is an intractable problem. To circumvent this problem, we will develop a number of techniques.
- By defining storing the water particles in a 3x3x3 oct-tree like data
structure, we can compute only the interactions between a particle
and the particles in the cells surrounding it.
This reduces the complexity from O(n2) to O(nk) where k<<n is roughly the number of particles in each of the cells in the lowest level of the 3x3x3 tree. - By keeping a measure of the total energy of the water particles within
each cell of the 3x3x3 tree and recursivly computing this total up the tree,
we can determine where our computation should be spent. This will allow us to
update nearly stationary particles less often, and concentrate one places where
particle interactions are strong.
- We will keep some neighborhood statistics, such as flux and curl, for each cell.
These will be used to alter the type of computations we perform on the
particles.
For example, in neighborhoods with little or no curl it may be sufficient to simply move each particle by its velocity vector, rather than considering its interactions with other particles. This dropping the complexity down to O(n). -
 For simulations of large volumes of water which in reality contain numbers of
particles on the order of Avagadro's number (10.023 x 1023), we plan
to instead model clusters of water molecules similar to
J. Stam
and E. Fiume
("Turbulent Wind Fields for Gaseous Phenomena". Proceedings of SIGGRAPH '93: 369-376.)
.
For simulations of large volumes of water which in reality contain numbers of
particles on the order of Avagadro's number (10.023 x 1023), we plan
to instead model clusters of water molecules similar to
J. Stam
and E. Fiume
("Turbulent Wind Fields for Gaseous Phenomena". Proceedings of SIGGRAPH '93: 369-376.)
.
This will perhaps, require new rules for particle interaction which more accurately reflect the interactions between large numbers of molecules.
RENDERING
RENDERING
Karl Sims showed an effective waterfall simulation (Particle Animation and Rendering Using Data Parallel Computation". Proceedings of GIGGRAPH '90: 405-413.) which was rendered with an accumulated raytracing algorithm. This is accomplished by passing a ray through the scene accumulating information as the ray passes through particles. The accumulated information is used to assign color and transparency. This is effective for a system where there is no global structure to the water, but it is of no use if you wish to have many of the effects associated with water(i.e. transparency, reflection, refraction, etc.).
These effects can be realized if the surface of the water is obtained. Many have accomplished this for a two-dimensional mesh(see Relevent Work Section below). A two-dimensional mesh is unrealistic, because when water is disturbed it is quite likely that it cannot be shown as a continuous surface in x and y.
We propose a method for doing this for the general case. Simply:
- Sort the particles in space(our oct-tree is already implemented)
- Move a plane through the environment. For each position of the plane:
- Create the bounding regions between different classes of particle
- Smooth the bounding regions based on particle class
- Assign relative index of refraction, color, opacity, shininess, displacement, and texture to region boundary
- Recreate a three-dimensional mesh surface using adjacent two-dimensional mesh surfaces
- Run a raytracing algorithm
This should give smooth, three-dimensional meshes around regions of particles. This makes possible the formation of artifacts like water-droplets, condensation, air bubbles in water, and turbulent surfaces. Also we can change the fluid properties to change water to blood, mercury, or coffee.
The Real Thing

|

|
|
|
| ||
|---|---|---|
MODELING DYNAMIC FLUID FLOW
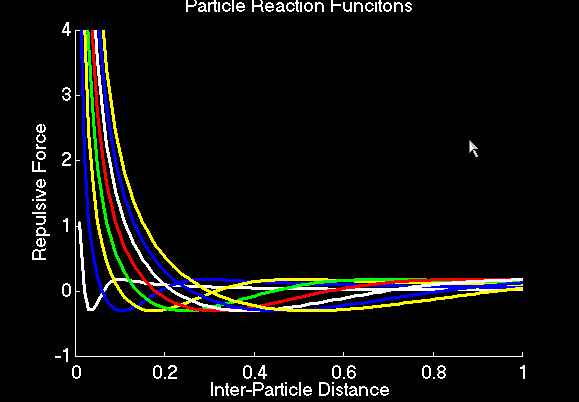
Figure 1.1:
|
The interactions between particles is based upon the class of curves of depicted above. A hyperbolic curve (d/x) encapsulates the repulsive van der Wells forces between groups of water molecules. A Gaussian, with mean d and standard deviation d*2 encapsulates the hydrophilic interactions which attract the molecules to one another. The parameter d is known as the principal distance, and is the distance at which two particles will be in equilibrium. The variation between curves is given by the parameter d, which is also abcissa of the zero crossing of the curve. Repulsion is given by d/x + exp ((d-x)^2/4*d^2).
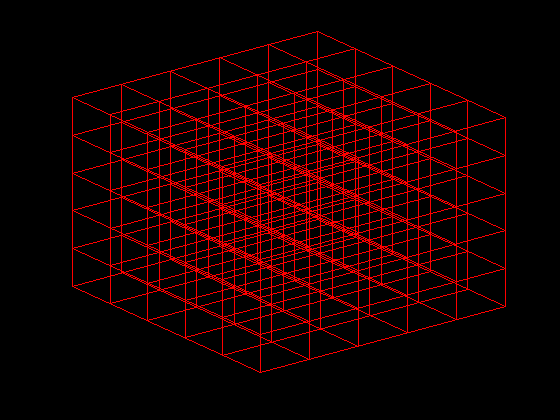
Figure 1.2:
|
|
Though specific physical arrangements are coded in our modeling language (c++),
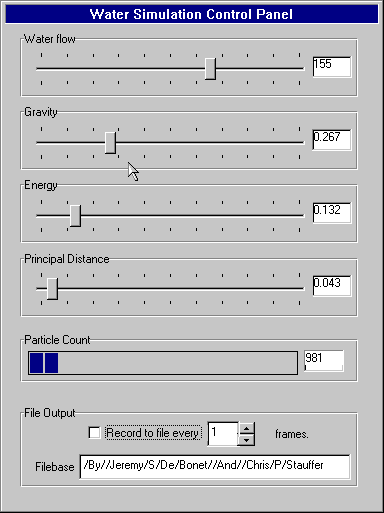
it is useful to control several dynamic factors during simulation time.
This control allows the simulator to achieve different sorts of effects, and flow
patterns.
Since there are 10.02323 molecules in only 18 grams of water, we must
model clusters of particles.
Given varying amounts of available computing power however, one may want to vary
the accuracy with which we model.
|
Interactions Between Particles and the Environment
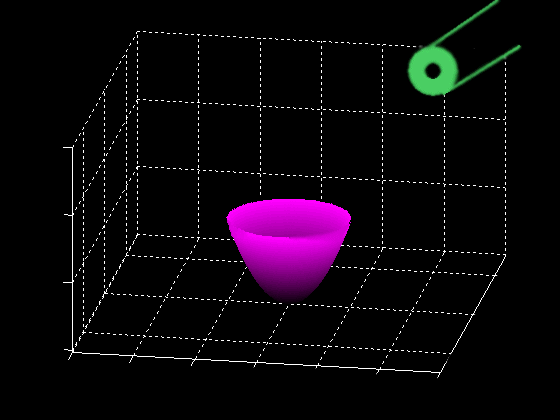
Figure 1.4:
|
Like light rays fired into a scene, particle in a simulation collide with and bounce off of objects in the environment. Unlike light however, particle velocities are not constant and are not so large that they can be considered instantaneous. In addition, forces such at gravity and collisions with other particles can change the path and velocity of a particle. Therefore when modeling the steps taken by particles, they are because of the very nature of computer simulation, discrete. To further complicate matters, motion of non-particle environmental objects may create sweeping changes in paths of particles.We have solved these problem in a unique way. Instead of considering collisions, which requires extensive testing when changes occur (O(n2) in general), we define a relationship operation between particles and surface. For example a particle could be inside a cylinder, outside a box or abovea plane. Then, when a move occurs, we insure that all particles retain the same relationship with respect to each surface. |
One can imagine more complex relationships as well, for example relationships which are the analog of constructive solid geometry, i.e. inside a cone and to the left of a plane. These "constructive hollow geometry" relations can result in more complicated interactions, because relationships between particle and surface can be changed. For example consider a particle on the inside part of a hemisphere which can be thought of as "inside a sphere and below a plane". In this case, a particle can legally pass out of this relationship by moving out of the open half. So a more applicable definition of its state is "retain relationship when inside the sphere and below the plane and absolve relation when above the plane".
When a relationship which should be retained has been violated, a classical collision
computation can then be performed to determine the correct bounce / reflection reflection
of the particles off of the surface so that their relationship can be maintained.
|
Sequence 1: Wine Glass
|
This is the simulation a bottle pouring liquid into a hemisphere. The bottom plane will be rendered as a table and the hemisphere as a wine glass. The viable flow rate will allow a synthetic rendering to be registed to the motion of the liquid particles.
|
Sequence 2: Kitchen Sink
This is a simulation of water in a kitchen sink. The stationary source will be registed to the rendering of the sink faucet. The simulation bounding box will fix the registration for the sink basin.
|
|
Rendering Video Sequences
Fluid is modeled by the particle system outlined above. Explicit knowledge of the obstructions in each scene is given to the modeler by defining combinations of constraining primitives(spheres, planes, cylinders).
The particle system outputs the water as a "blob" composed of spherical components corresponding to each of the water particles. "Blobs" are iso-surfaces of scalar fields defined by each component given its strength.
The spherical components are streched in the direction of the motion an amount corresponding to the magnitude of the motion. This helps flatten standing water and thin streams of water.
The following two video sequences were rendered using POVRay, a public raytracing package freely available for most computer systems. By clicking on each image, the corresponding video can be viewed.
Sequence 1: Wine Glass
 |
|
|
| |
|---|---|
This is a model of a bottle pouring wine into a glass on a marble table. The light sources are above the table and in the lamp. The labels show that this is a fine vintage MIT wine.
The table is modeled as a plane. The cup is modeled as half of a sphere. The bottle angle is determined by the flow rate in the modeler. The wine within the bottle is not composed of particles but, rather, is defined as a the interior of the bottle which would be filled given a certain amount of wine. This does not change over time, but could.
Sequence 2: Kitchen Sink
 |
|
|
| |
|---|---|
This is a model of water in a kitchen sink. Temporal aliasing resulting from a lack of randomization of the initial particles is visible in the video.
The source of the water is the faucet. The region is bounded by a box the size of the sink.
The Task of Rendering
On some machines, each frame could take hours to render. This could cause problems if you had to create video sequences involving hundreds of frames. Our solution to this problem was to obtain an automatically generated list of all the SunOS computers in the AI Lab and use that to distribute the rendering. This allowed us to start 166 rendering jobs simultaniously.
|
Jeremy S. De Bonet jsd@debonet.com |

|
|
|
|