|
I've developed a dictionary based universal compression
scheme which is able to achieve high compression rates in situations
where Lempel-Ziv type techniques fail.
Lempel-Ziv techniques utilize string matching to reduce the code length
of commonly occuring strings. This works well for text and some other types
of data which consist of a small symbol alphabet.
Because the dictionary construction techniques build and reuse common strings quickly,
for text data, these methods reach bit rates which quickly approach the true entropy
of the source.
However, in data which can take on values over a large range (i.e. a large alphabet)
-- as is the case with sounds and images -- sequences of symbols are rarely
repeated exactly, but are often repeated approximately. As a result few string matches
are found by LZ techniques, and it takes a lot of data to build up a dictionary of long
phrases. LZ methods are universal, so they eventually will achieve compression at the true
entropy of the source, but could take an arbitrarily long time to do so.
Since we care about finite length data, the rate of convergence to the true
entropy is important.
LZd (for Lempel-Ziv differential) is dictionary based universal compression
scheme which uses approximate string matches to compress data such as images
and sounds.
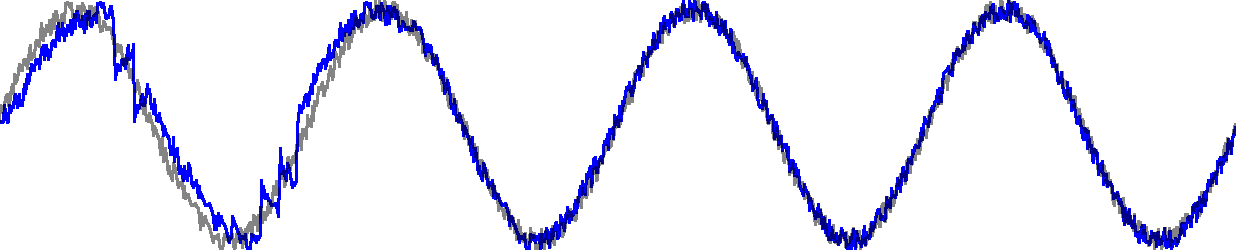
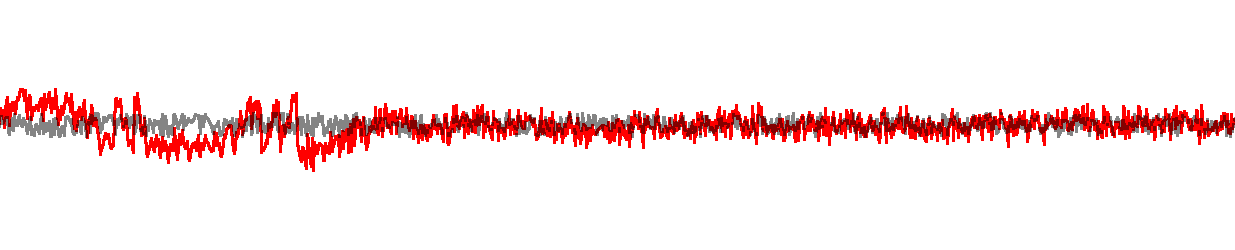
At the heart of LZd is a balancing act between building long phrases which
approximately match the signal, and the cost encoding the residual error of
the approximate match.
|